AI Search Algorithms Implementations
in Articles
In Naboo Planet the R2-D2 droid is serving her Queen Amidala and has received some important documents of Dark Lord Darth Vadar.
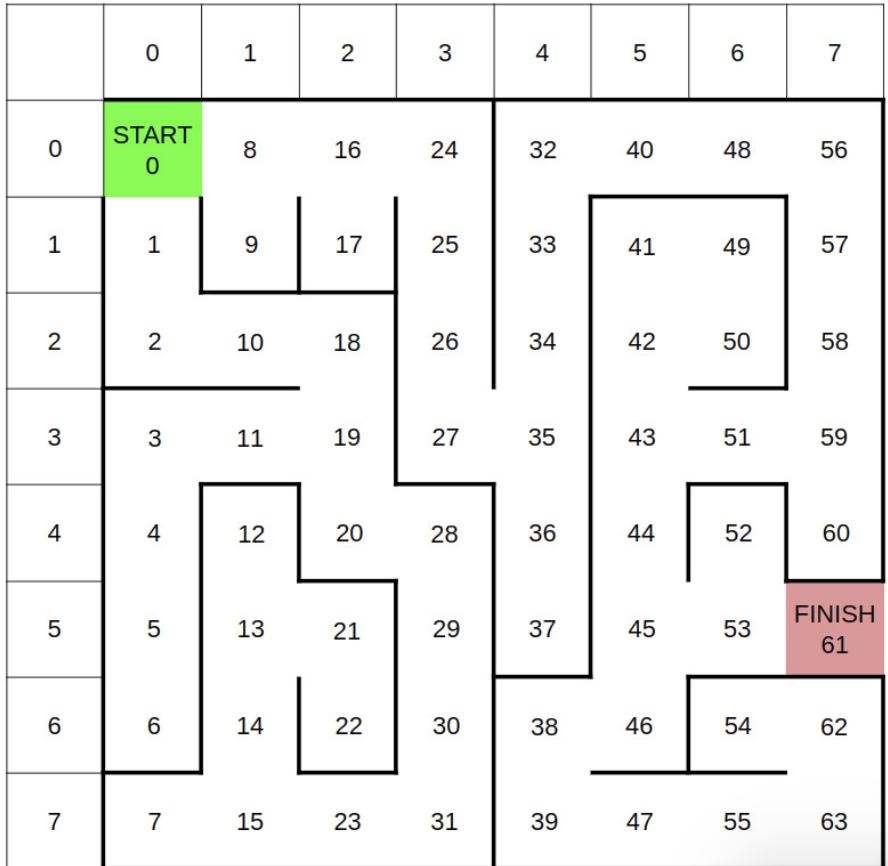
As soon as Dark Lord finds this out, he sends his army after R2D2 to recover the documents from him. Fearing the Darth’s Army, R2D2 hides in a Cave. While entering the cave R2D2 has found a map of the cave and It knows that it is at grid location 0 and needs to reach grid 61 to go out of the Cave.
Darth’s Army has got to know that R2D2 is hiding in the cave and set up the explosives in the cave that will go off after a certain time.
Let us use our knowledge of AI and help R2D2 to search his path out of the Cave.
R2D2 will follow the following rules for Searching the cave(which are hardcoded in his memory)
- The (x, y) coordinates of each node are defined by the column and the row shown at the top and left of the maze, respectively. For example, node 13 has (x, y) coordinates (1, 5).
- Process neighbours in increasing order. For example, if processing the neighbours of node 13, first process 12, then 14, then 21.
- Use a priority queue for your frontier. Similar to Assignment 2, add tuples of (priority, node) to the frontier. For example, when performing UCS and processing node 13, add (15, 12) to the frontier, then (15, 14), then (15, 21), where 15 is the distance (or cost) to each node. When performing A*, use the cost plus the heuristic distance as the priority.
- When removing nodes from the frontier (or popping off the queue), break ties by taking the node that comes first lexicographically. For example, if deciding between (15, 12), (15, 14) and (15, 21) from above, choose (15, 12) first (because 12 < 14 < 21).
- A node is considered visited when it is removed from the frontier (or popped off the queue).
- You can only move horizontally and vertically (not diagonally).
- It takes 1 minute to explore a single node. The time to escape the maze will be the sum of all nodes explored, not just the length of the final path.
- All edges have cost 1.
Uniform Cost Search
If R2D2 uses a Uniform Cost Search, how long will it take him to escape the Cave?
Below is the Pseudo code of Uniform Cost Search

Let us try to implement the Uniform cost search
def uniform_cost_search(graph, start, goal):
path = []
explored_nodes = list()
if start == goal:
return path, explored_nodes
path.append(start)
path_cost = 0
frontier = [(path_cost, path)]
while len(frontier) > 0:
path_cost_till_now, path_till_now = pop_frontier(frontier)
current_node = path_till_now[-1]
explored_nodes.append(current_node)
if current_node == goal:
return path_till_now, explored_nodes
neighbours = graph[current_node]
neighbours_list_int = [int(n) for n in neighbours]
neighbours_list_int.sort(reverse=False)
neighbours_list_str = [str(n) for n in neighbours_list_int]
for neighbour in neighbours_list_str:
path_to_neighbour = path_till_now.copy()
path_to_neighbour.append(neighbour)
extra_cost = 1
neighbour_cost = extra_cost + path_cost_till_now
new_element = (neighbour_cost, path_to_neighbour)
is_there, indexx, neighbour_old_cost, _ = get_frontier_params_new(neighbour, frontier)
if (neighbour not in explored_nodes) and not is_there:
frontier.append(new_element)
elif is_there:
if neighbour_old_cost > neighbour_cost:
frontier.pop(indexx)
frontier.append(new_element)
return None, None
So, If R2D2 follows the Uniform cost search, 58 nodes will be explored and hence it will take 58 mins for him to get out of the cave.
Turns out that the Darth Vadar also has the knowledge about the UCS, he updated the time of the explosive so that UCS will not work anymore for R2D2.
What choice does R2D2 have now?
Having studies Search Algorithms, R2D2 knows that A* search works faster than Uniform cost search. He uses A* search with the Manhattan distance heuristic. How much time will R2D2 take now to find the path out of the cave?
A Star Search
Let us implement the A star Search algorithm with the Manhattan distance heuristic.
Manhattan distance is the sum of the horizontal and vertical distances between points on a grid and the formula to calculate the same is:
def get_manhattan_heuristic(node, goal):
i, j = divmod(int(node), 8)
i_goal, j_goal = divmod(int(goal), 8)
i_delta = abs(i - i_goal)
j_delta = abs(j - j_goal)
manhattan_dist = i_delta + j_delta
return manhattan_dist
def astar_search(graph, start, goal):
path = []
explored_nodes = list()
if start == goal:
return path, explored_nodes
path.append(start)
path_cost = get_manhattan_heuristic(start, goal)
frontier = [(path_cost, path)]
while len(frontier) > 0:
path_cost_till_now, path_till_now = pop_frontier(frontier)
current_node = path_till_now[-1]
path_cost_till_now = path_cost_till_now - get_manhattan_heuristic(current_node, goal)
explored_nodes.append(current_node)
if current_node == goal:
return path_till_now, explored_nodes
neighbours = graph[current_node]
neighbours_list_int = [int(n) for n in neighbours]
neighbours_list_int.sort(reverse=False)
neighbours_list_str = [str(n) for n in neighbours_list_int]
for neighbour in neighbours_list_str:
path_to_neighbour = path_till_now.copy()
path_to_neighbour.append(neighbour)
extra_cost = 1
neighbour_cost = extra_cost + path_cost_till_now + get_manhattan_heuristic(neighbour, goal)
new_element = (neighbour_cost, path_to_neighbour)
is_there, indexx, neighbour_old_cost, _ = get_frontier_params_new(neighbour, frontier)
if (neighbour not in explored_nodes) and not is_there:
frontier.append(new_element)
elif is_there:
if neighbour_old_cost > neighbour_cost:
frontier.pop(indexx)
frontier.append(new_element)
return None, None
R2D2 now explored 50 nodes and hence it now takes 50 minutes to get out of the cave, which is 8 minutes faster than the UCS.
R2D2 now got a tip from a trusted droid friend that Darth Vadar has once again updated the timer and that a traditional A* search will not be good enough.
R2D2, being the expert he is, is not deterred. He notices there is a bottleneck in the maze. More specifically, the edge from 27-35 is the only way to crossover from the left half of the maze to the right half.
Realizing this, R2D2 decides to split the search into two parts. First, he searches from the start to the bottleneck (node 27). Then, he searches from the bottleneck (node 35) to the goal. How much time will he take to get out of the cave now?
If R2D2 run the bottleneck Astar from 0 to 27 and then 35 to 61, he just needs to explore 38 nodes and can get out the cave quicker as compared to the other search methods.
Conclusion
As we can see in the results above, A* Search algorithm is really a “smart” search algorithm and works faster as compared to other conventional search algorithms. And it is also worth mentioning that many games and web-based maps use this algorithm to find the shortest path very efficiently.
The code used in this article and the complete working example can be found the git repository below: https://github.com/fakemonk1/AI-Search-Algorithms-Implementations